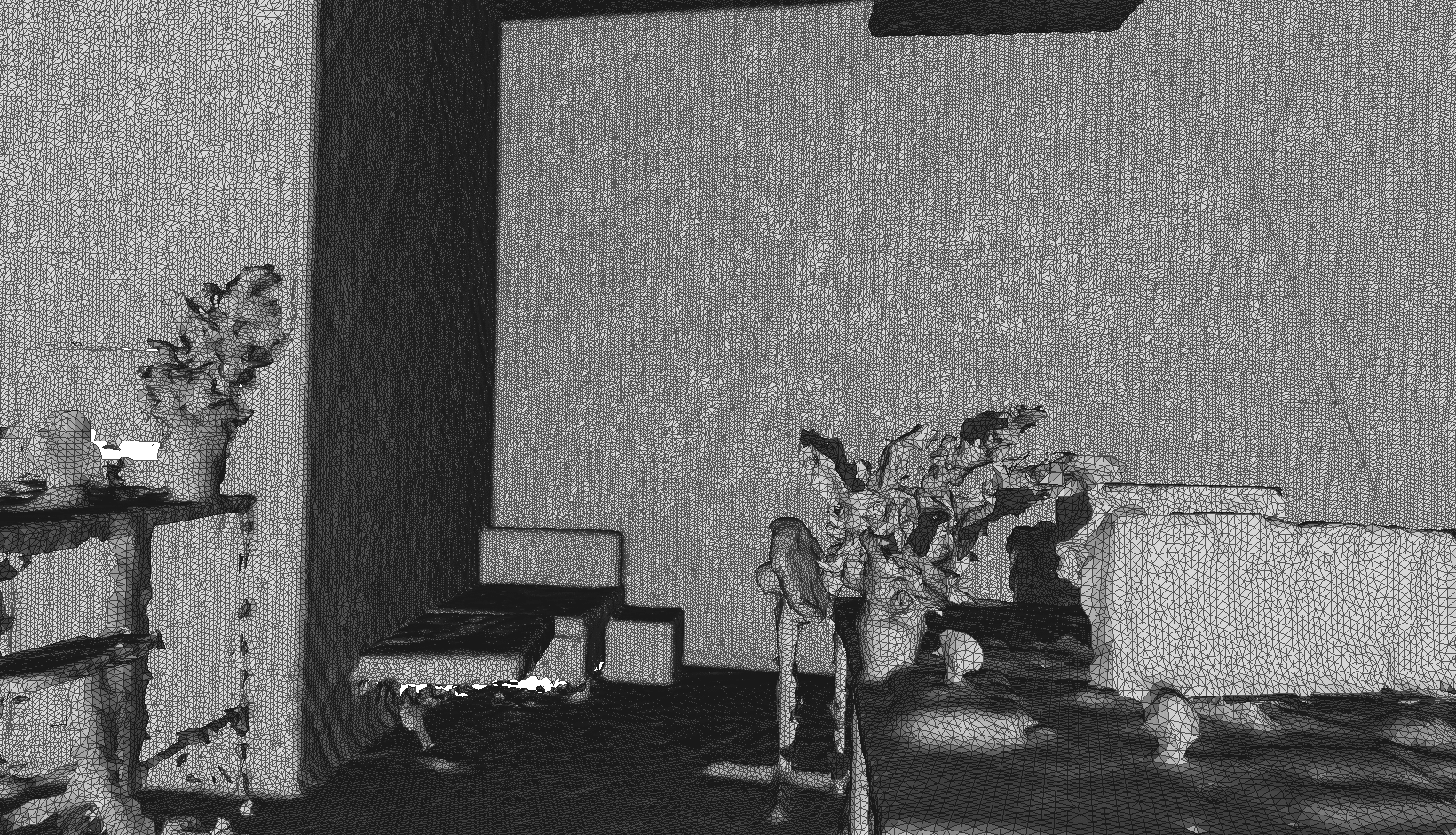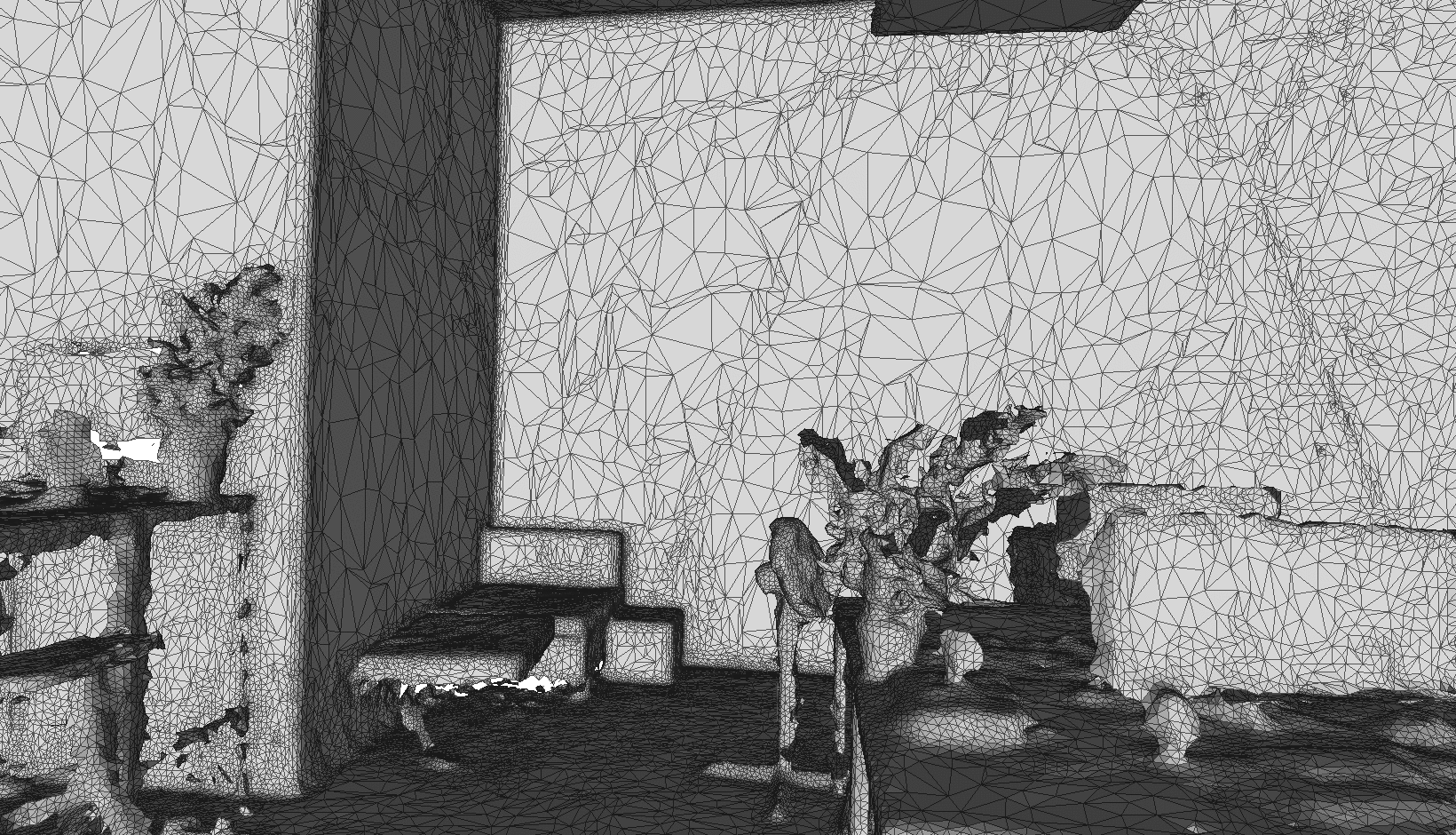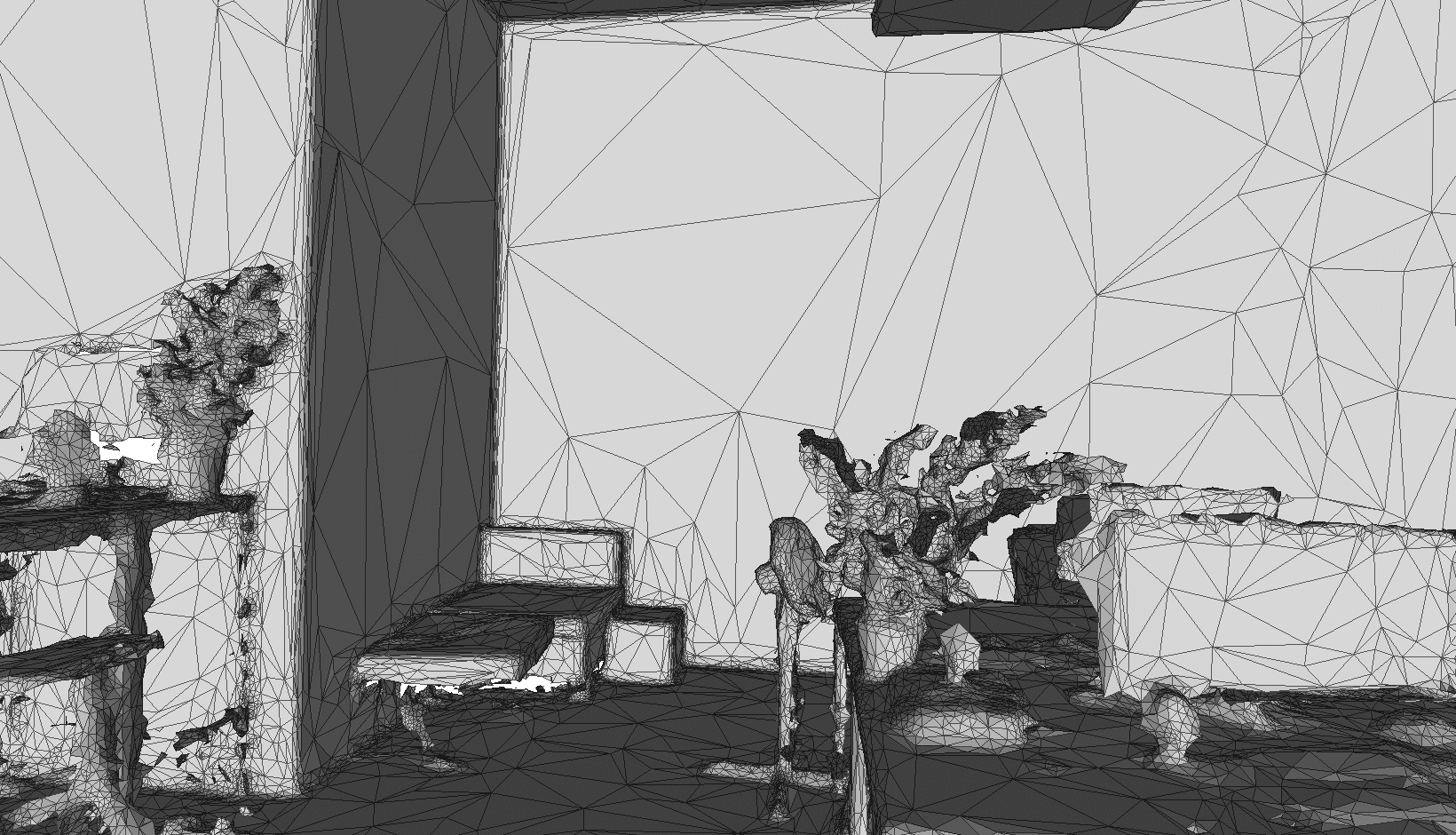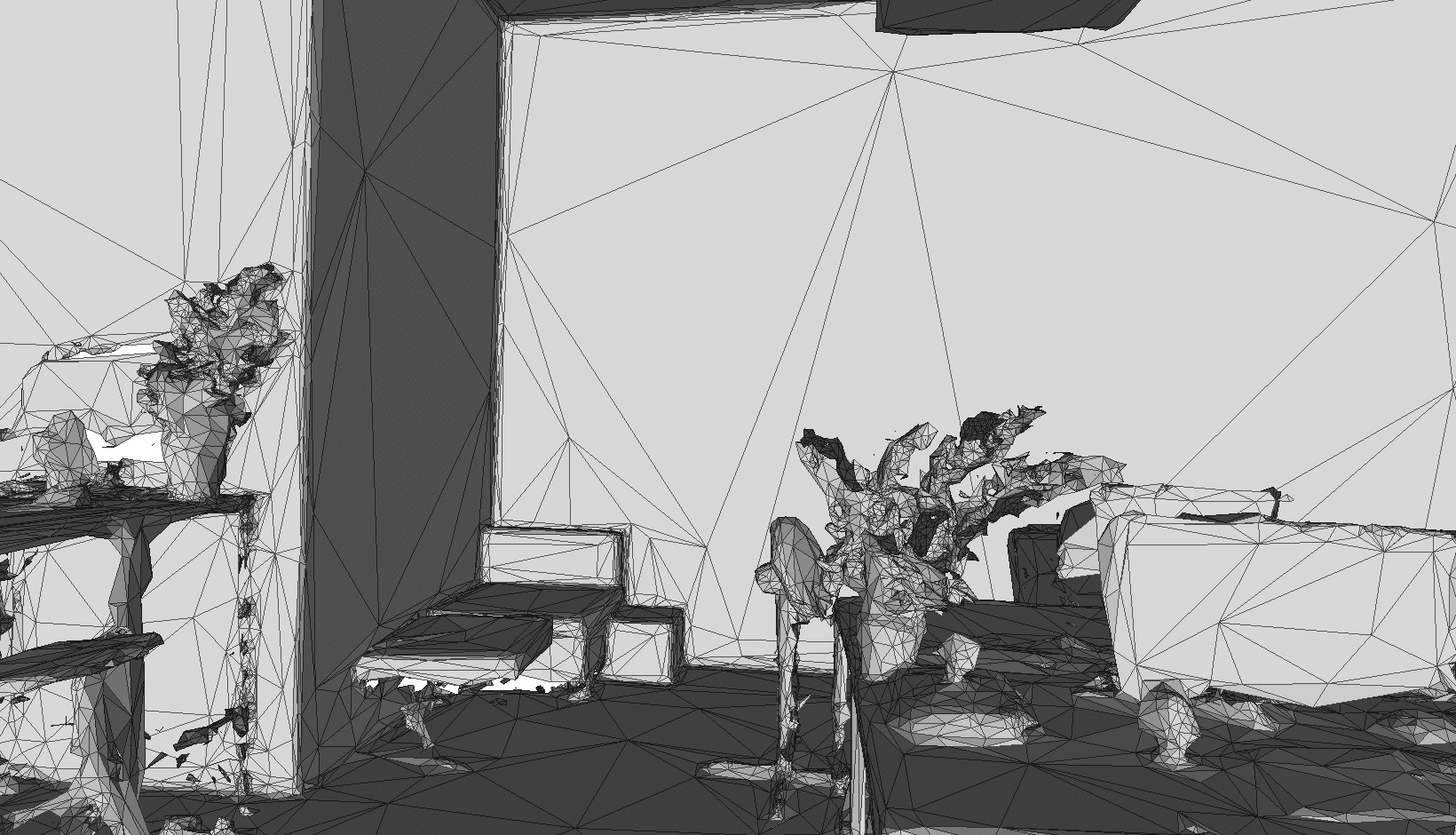Parallel Mesh Simplification For Planar Surfaces

This work elaborates a parallel algorithm based on quadric error metric and adaptive thresholding to simplify a triangle mesh. The approach emphasizes planar surfaces as a target to simplify. The main goal was to create a framework able to produce high-quality progressive meshes based on reconstructed ones from the environment. Those meshes are characterized by constant resolution of reconstruction, therefore storing vertices for planar surfaces evenly across the shape, which is not necessary.

This project elaborates a specific case of mesh simplification, where the focus is mostly on planar surfaces, like walls and floors, at the same time, keeping a high level of details for complex shapes; plants, elements on desks in an office, etc. Mesh reconstruction in general introduces the problem of using the same level of details for the whole 3D space. Most of the planar surfaces can be described with a reduced amount of triangles. Therefore, after generating a reconstructed mesh from real-world environments, mapped by static or mobile scanners, we can successfully apply simplification with great results. In the next chapter, I will elaborate on the foundations for the geometric error metric. Forwarded by the introduction to the extended version of this algorithm, which additionally uses color and normals for the error metric. Finally, in the fourth chapter, I will describe the parallel approach with adaptive thresholding to solve the problem.

The code can be found in the repository.