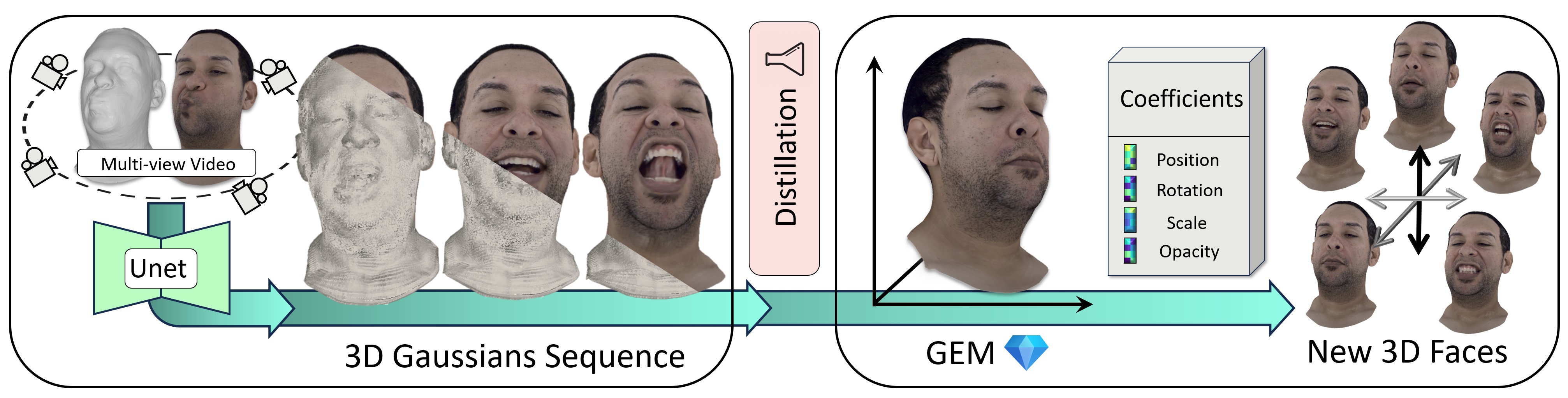
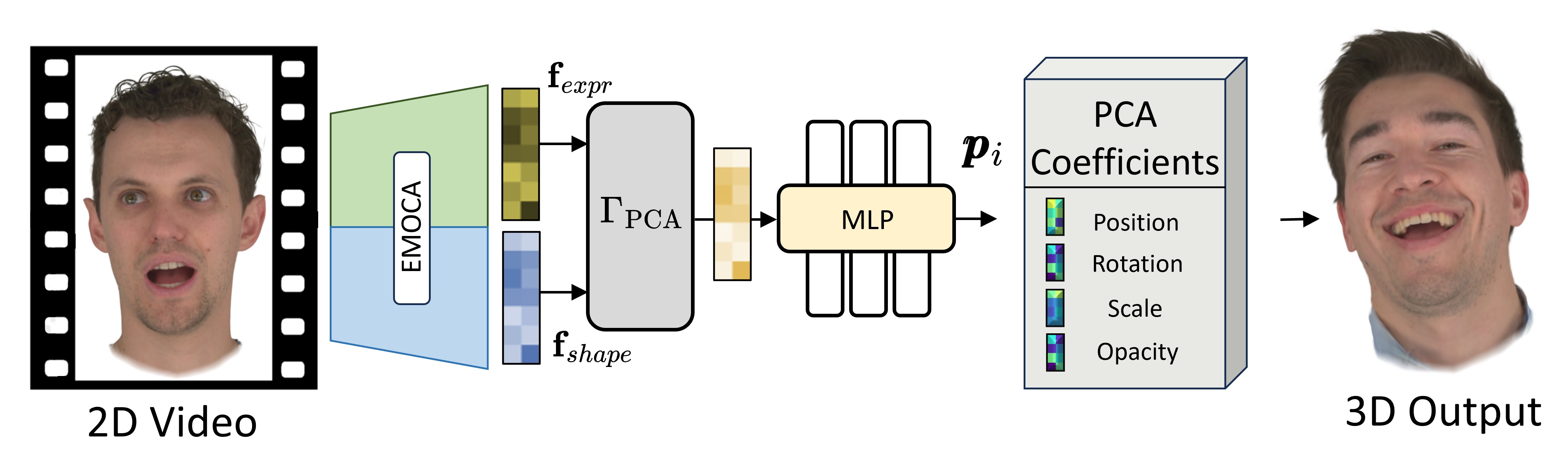
Current personalized neural head avatars face a trade-off: lightweight models lack detail and realism, while high-quality, animatable avatars require significant computational resources, making them unsuitable for commodity devices. To address this gap, we introduce Gaussian Eigen Models (GEM), which provide high-quality, lightweight, and easily controllable head avatars. GEM utilizes 3D Gaussian primitives for representing the appearance combined with Gaussian splatting for rendering. Building on the success of mesh-based 3D morphable face models (3DMM), we define GEM as an ensemble of linear eigenbases for representing the head appearance of a specific subject. In particular, we construct linear bases to represent the position, scale, rotation, and opacity of the 3D Gaussians. This allows us to efficiently generate Gaussian primitives of a specific head shape by a linear combination of the basis vectors, only requiring a low-dimensional parameter vector that contains the respective coefficients. We propose to construct these linear bases (GEM) by distilling high-quality compute-intense CNN-based Gaussian avatar models that can generate expression-dependent appearance changes like wrinkles. These high-quality models are trained on multi-view videos of a subject and are distilled using a series of principal component analyses. Once we have obtained the bases that represent the animatable appearance space of a specific human, we learn a regressor that takes a single RGB image as input and predicts the low-dimensional parameter vector that corresponds to the shown facial expression. In a series of experiments, we compare GEM's self-reenactment and cross-person reenactment results to state-of-the-art 3D avatar methods, demonstrating GEM's higher visual quality and better generalization to new expressions.

Video
BibTeX
@inproceedings{zielonka2024gem,
title = {Gaussian Eigen Models for Human Heads},
author = {Wojciech Zielonka and Timo Bolkart and Thabo Beeler and Justus Thies},
booktitle = {CVPR},
month = {June},
year = {2025},
}